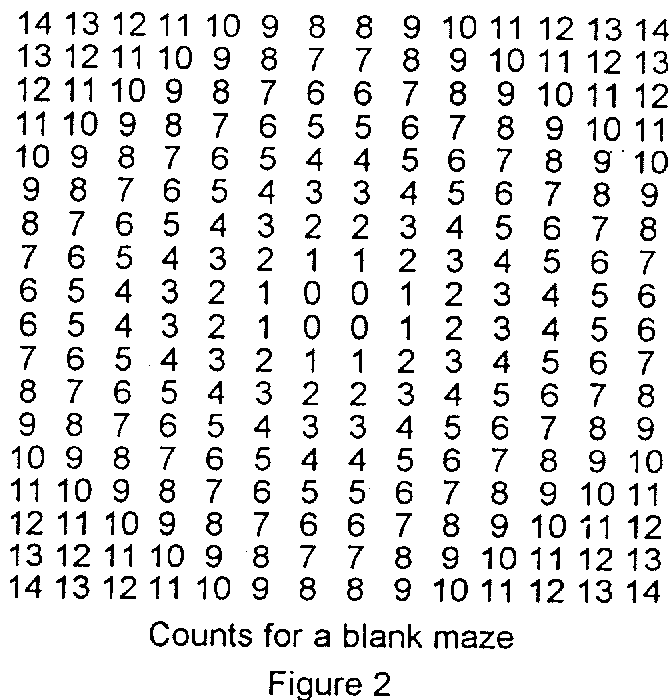|
|
Real-time maze solving This is a copy of a paper presented at EuroFORTH 97 by Duncan Louttit.
This paper discusses strategies for solving the mazes used in the IEE Micromouse championship. These mazes are built of 5 cm high walls on an 18 cm grid in a 16 by 16 square i.e. 256 cells. The walls are12 mm thick and painted red with white tops. The floor is black. The target is the four central squares. The start point is the "bottom left-hand corner". All grid points, except the centre one are guaranteed at least one wall going to them.
The outside of the maze is a continuous wall. The maze is designed so that it cannot be solved by a "follow the left-hand wall" algorithm. A typical maze is shown in figure 1.

figure 1
The object of the exercise is to build a robot "mouse" that can getfrom the start to the centre in the shortest possible time. "Run time" is the time taken to get from the start to the centre. "Search time" spent exploring the maze is penalised by 1/30th of the total time spent in the maze prior to the start of the run. You can have many runs within a time limit of 15 minutes.
Mice must be self-contained. They need to carry their processors,motors, sensors and batteries with them.
This type of application where "real-time" is measured by racing against other competitors and resource costs in terms of weight, size and power consumption directly affect the capability of the mouse seems to be an ideal application for FORTH. Most mice currently use assembly language for optimum performance but there are now a couple of FORTH mice that successfully run the maze.
My mice use 8031 processors expanded to 32K EPROM and 32K RAM. This is overkill in memory space but, once you expand memory you might as well use the biggest capacity devices that come to hand. I use MPE's version 5 Powerforth compiled on a PC.
Strategy One My first solver was intended to be the simplest and quickest algorithm that I could devise that was guaranteed to solve the maze. It is quick in terms of computation time rather than optimising the search time or finding the shortest route.
A little thought showed that all one had to do was make good choices at the decision points in the centre of the maze cells. A mouse has the choice of going straight on, turning either way or, only needed during the search phase, turning right round. Obviously the mouse should only make choices that are not blocked by walls.
I wanted a simple algorithm that makes sensible choices that eventually lead to the centre of the maze without making the mouse wait for long at each decision point. It became clear that I would need some kind of "map" to carry information from previous choices to help with the current choice.
I ended up with a set of three rules. They are:-
The mouse should prefer to go to cells it has visited the minimum number of times. This requires that the map should hold a count of how many times each cell has been visited. These counts are initialised to 0. This is the only map information needed.
The mouse should prefer to get closer to the centre of the maze. This is done with a table of distance counts. These are initialised at compile time.
The mouse should prefer to travel in a straight line as this is quicker!
These rules are sufficient to solve any Micromouse maze but the mouse may spend a lot of time traversing "lobster pots" where it cannot find the exit from the trap until it has gone round many times.
I used this algorithm on two DASH micromice and each was able to solve mazes in competition. It uses few computing resources, is easy to explain, and does not compromise the speed of the mouse when it is travelling between decision points. As far as I know it is unique.
Strategy Two This is the algorithm used by most contestants and is guaranteed to find the shortest route through the maze. Unfortunately, it is computationally intensive and I offer my code as one reasonably quick way to do the job in a high-level language.
The algorithm is based on the concept of page 90 of "Thinking FORTH".
What you do is count back from the target until you find a route. The centre cells have the value 0, cells that are adjacent to these with no wall in the way have the value 1, cells that are adjacent to cells with value 1 and with no wall in the way have the value 2 etc. As the mouse explores the maze it discovers more and more maze wall positions and uses this information to generate new sets of counts.
All the mouse has to do at a decision point is choose to go to a cell with a lower count than the current one, provided it is not blocked by a wall.
The algorithm starts with the four target cells initialised to count values of 0. All other cells are initialised to 255 (the maximum possible value).
Each cell has four neighbours. If there were no walls the correct count for that cell should be one more than the lowest count of its four neighbours. The presence of walls means that some neighbours should not be taken into consideration.
The mouse's map of the maze starts with only the outside walls present. The others are filled in as the mouse finds them.
In one pass, the search algorithm looks at each of 256 cells and, from each one, evaluates the contents of its neighbours and changes its count as necessary.
Starting from the initial conditions, it takes 14 passes of the algorithm to propagate a count (14) back to the start square. The counts then are shown in figure 2.
I use just one array of counts for the maze rather than having a separate array to put the new counts in when they are generated. Cells to the South and West of the current cell will have been changed by the algorithm before it operates on the current cell. This makes wall effects propagate faster upwards and to the right. (Maze designers may choose to design their mazes to make this less helpful. The competition is a contest between maze designers and competitors!)
In a pathological case it may take a large number of passes of the algorithm to find the optimum path. I think that it may be possible to design a maze that takes 128 passes to solve.
So, in a worst case, the algorithm would have to evaluate the minimum out of four cell counts for each of 256 cells for 128 passes of the algorithm each time the mouse moves one cell! If this was done at every decision point, the mouse would move a cell, wait for many seconds and then move to the next cell. This is a big disadvantage compared to strategy one. Remember that the mouse is a physical object and cannot accelerate up to speed or stop instantly.
Fortunately, the search algorithm can run as a background task while the mouse runs between cells. As long as the counts have been updated by the time the mouse reaches the next decision point, all will be well.
If the algorithm is run as a background task while the mouse is moving,it is very important that the amount of time it takes on each invocation is consistent. I use it as a delay loop in my wall-following control system, so it is vital that it does not change significantly in execution time depending on the number and distribution of maze walls.
It is not practical to run 128 passes of the algorithm between decision points on my system. Perhaps a couple of Pentiums could manage it but I don't have the electrical or mechanical power or size to run these! Fortunately it is not necessary to wait for full optimisation to get a good decision. A single pass is not sufficient as, after the mouse detects a dead-end, the changing counts only propagate at the same rate as the mouse moves so the current cell has the same count as the one it should go to next. I use two passes of the algorithm during the time that the mouse moves one cell.
So, the implementation must not only be fast enough to leave some processing cycles for other purposes when the mouse is moving, but must also take a consistent time whatever the data (maze) is. This seems to me to be a good definition of real-time!
To make for consistent run times I avoid IF almost completely. The only decisions I use (nearly) are embedded in MIN. The implementation of MIN is in code and is nearly consistent for both routes. If my control system was damaged by small timing errors, I would need to re-code MIN for exact consistency.
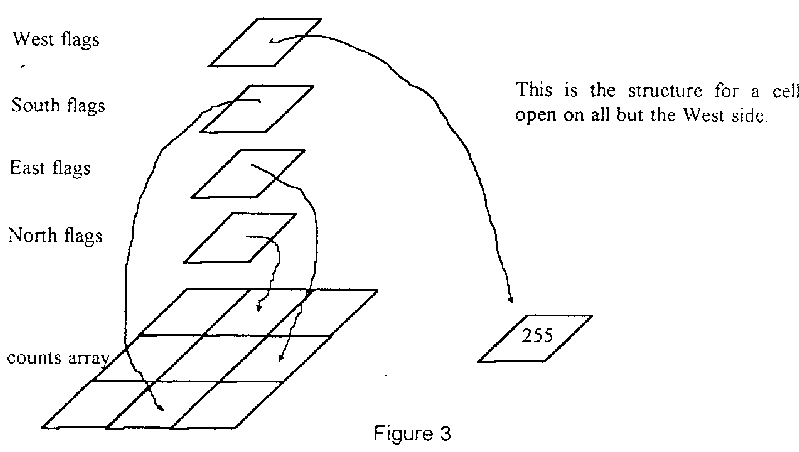
The implementation uses indirection to achieve the desired result. I use a word array for the cell counts and four word arrays that deal with the wall information from the maze. Each maze cell has an element for the cell count plus an element in each of the wall flag pointer arrays for the corresponding North, South, East and West walls. There are 16 spare elements to deal with the edges of the maze.
Each flag pointer either points to the corresponding cell count or to an address that holds 255. The corresponding cell for the North flag is the cell North of the cell under consideration. The other flags point to the appropriate cells. When a wall is detected, the flag pointer is changed to point to 255. (see figure 3). So, to find the new count value for a cell, all I have to do is fetch the values of the adjacent cells via the flag pointers, take the smallest of them, and add 1. NO DECISIONS HAVE TO BE MADE!
Where a wall is present, the value returned will be 255. This is always bigger than the true new value for the cell, so it will be lost in the process of finding the smallest neighbour value.
There is a problem with this approach. The target cells in the centre start off with the value 0. On the first pass, these cells would detect that their lowest neighbour value was 0 and consequently they should have their count increased to 1. On each subsequent pass the count would increase. To avoid this problem I check to see whether the count is 0 before generating a new count. If it is 0, I do nothing, but I take care to balance the time taken to do nothing so that no problems are caused. This is the only IF in the algorithm.
This system works, but is still slow. I made a new assembler definition to give a double indirection, @@, that speeds things up a little. I also need a defining word that would allow assembly speed addition of a constant. I made one that works O.K. when compiled in the target but I have not yet persuaded it to cross-compile.
Running Strategy Two The mouse runs the algorithm as a delay during the control system that moves the mouse on one cell. At each decision point, the mouse chooses whether to go straight on or turn. My mouse prefers to go straight on if possible, failing that, it prefers to turn right. When it reaches a cell with a count of 0, it knows it has reached the centre.
Once it has reached the centre, it may still not know the best route. It has another go at finding a good route on its way back to the start. It notes the count that is now in the start cell, resets all the array counts to 255, sets the start cell count to 0, and then runs the algorithm the number of times that was in the start cell when it reached the centre. This guarantees that the counts have propagated back from the start cell to the centre.
Then the mouse repeats the process that took it to the centre until it reaches the start. It can then have another go at reaching the middle. It may take many runs to find the best route, but it is guaranteed to find it eventually.
Results Unfortunately my hard disk crashed one week before the competition. The algorithm ran on the final hardware as a simulation with good results in terms of solving a sample maze. Due to the crash, it was not possible to complete system integration in time to run in competition.
However I was able to run strategy one again and came second (out of two!). It did solve two different mazes satisfactorily.
Had I been running strategy two, the times would actually have been slower. Due to the greater computational overhead, the cruising speed of the mouse would have been slower by some 20% and, as it happens the final maze could be solved by strategy one very easily. Strategy two is theoretically better but not if strategy one happens to find the best solution anyway. As you are not allowed to select strategies once you have seen the maze, strategy two is a safer bet. The real problem is second-guessing the maze designers!
Mouse limitations My current mouse is limited in performance by the processor speed. Either I must use a faster processor (I was beaten by an H8), I must recode in assembler (seems a shame) or I must find a more efficient coding for the strategy two algorithm. If you have suggestions, please let me have them.
At present, my thoughts for my next generation mouse are along the lines of using a "maze-solving co-processor" i.e. a second microprocessor dedicated to solving the maze. All the other functions are comparatively simple and need little memory, so I may end up with a single-chip 8031, e.g. one of ATMEL's finest, controlling the motors and sensors and passing wall information to the existing processor system at each decision point and getting turn commands back in exchange. This should be fast enough for the existing mechanics without being forced to use assembler.
In the experts class, mouse speeds can reach 1-2 metres/second. At these speeds, I really will need more processing power, assembly language coding or, just possibly, an even better algorithm!